1. 拓扑学

 

拓扑学（Topology）是一门新兴的几何学，作为几何学。 它仍是研究图形(或形状)的科学。 它之所以较新，是因为它研究的是图形在连续变形下的不变的整体性质。 与其它的几何学相比，它更为灵活和更具可塑性，所以有时又称做“橡皮板几何学”。 拓扑学与欧几里得几何学的不同之处在于它不涉及距离、方位或曲直等性质，即不涉及图形的量度性质。 例如，火车站的交通示意图、公共汽车站的路牌都可以看作拓扑图形，因为这些图形在比例、形状或位置方面均有着极大的变形。 在欧几里得几何学中，只允许图形做刚体运动(平移、旋转、反射)，在这种运动中，图形上任意两点间的距离保持不变，因此，这里的几何性质就是指那些在刚体运动中保持不变的性质，因而欧几里得几何学可叫做“刚体几何学”。 拓扑学中的运动可以称作“弹性运动”，对图形可以任意伸张、扭曲、拉缩，但图形中不同的各点仍为不同的点，不可能使不同的两点合并成一点。 当且仅当一图形做弹性运动使其与另一图形重合，这两个图形是“拓扑等价”的，一个图形的拓扑性质是那些与此图形等价的图形都具有的性质。 因此，图形的拓扑性质就是那些在弹性运动中保持不变的性质，一图形的任何弹性运动都丝毫不改变图形的拓扑性质，所以拓扑学也叫“弹性几何学”。

2. 拓扑关系

在地图上仅用距离和方向参数描述图上目标之间的关系是不圆满的。 因为图上两点间的距离或方向（在实地上是一定的）会随地图投影不同而发生变化。 因此仅用距离和方向参数还不可能确切地表示它们之间的空间关系。 并且，在地图图形的连续变换中，它的某些性质发生了变化，如长度、角度和相对距离，但另一些性质则保持不变，如邻接性、包含性、相交性和空间目标的几何类型(点、线、面特征类型)等保持不变。 这类在连续变形中保持不变的属性称为拓扑属性。

空间拓扑关系是讨论空间实体间拓扑属性，即在拓扑变换旋转、平移、缩放等下保持不变的空间关系，它是GIS中不可缺少的一种基本关系。 拓扑关系是不考虑度量和方向的空间实体之间的空间关系，拓扑学是研究图形在拓扑变换下不变的性质，因此拓扑学己成为空间拓扑关系研究的基础，为空间对象间的包含、覆盖、相离、和相接等空间关系的描述提供直接的理论依据。 地理空间中的点、线、面实体之间存在着各种各样的拓扑关系，因此表示拓扑关系的数据是空间数据的重要组成部分。 另外，空间拓扑关系是空间查询与分析的基础。 一方面它为地理信息系统数据库的有效建立、空间查询、空间分析、辅助决策等提供了最基础的关系，另一方面使空间拓扑关系理论应用于地理信息系统查询语言，形成一个标准的空间查询语言成为可能，从而通过应用程序进行空间特征的存储、提取、查询、更新等。

 

拓扑关系是指网结构元素结点、弧段、面域之间的空间关系，主要表现为下列三种关系：

（1）拓扑邻接

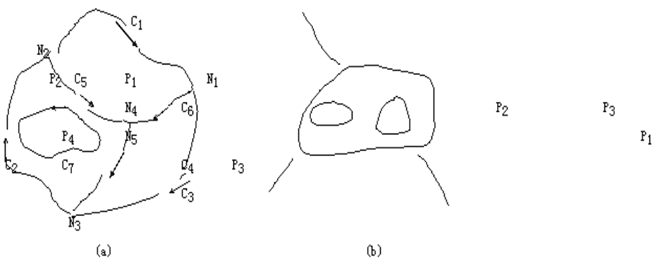
拓扑邻接指存在于空间图形的同类元素之间的拓扑关系。 如图(a)所示，结点邻接关系有N1/N4，N1/N2···等；多边形邻接关系有P1/P3，P2/P3 ···等。

（2）拓扑关联

拓扑关联指存在于空间图形的不同类元素之间的拓扑关系。 如图(a)所示，结点与弧段关联关系有N1/C1、C3、C6，N2/C1、C2、C5 ···等。 多边形与线段的关联关系有P1/C1、C5、C6，P2/C2、C4、C5、C7等。

（3）拓扑包含

拓扑包含指存在于空间图形的同类但不同级的元素之间的拓扑关系，如图(b)所示，P1包含P2和P3。

空间数据拓扑关系对地理信息系统的数据处理和空间分析具有重要意义。 根据拓扑关系，不需要利用坐标或距离，可以确定一种地理实体相对于另一种地理实体的位置关系，拓扑数据也有利于空间要素的查询，例如，查询某铁路线有哪些车站，汇入某条主流的支流有哪些，以某个交通“结点”为中心，呈辐射状的道路各通向何地。

3. 拓扑数据结构

在矢量拓扑数据结构中，空间数据不但要记录空间实体的位置，而且要记录空间实体间的拓扑关系，这是地理信息系统区别于其它数据库管理系统的重要标志。 建立拓扑关系是一种对空间结构关系进行明确定义的数学方法。 目前，空间数据的拓扑数据结构的表示方式没有固定的格式，也还没有形成标准，其基本原理是相同的。 因此，在矢量拓扑结构表示方法中，任何地理实体均可以用点、线、面来表示其特征，并且可根据各实体间的空间拓扑关系，解译出更多的信息。

对于二维空间数据而言，矢量数据可抽象为点（结点）、线（弧段或边）、面（多边形）三种要素，也称拓扑要素。 对三维而言，还要加上体。 其最基本的拓扑关系主要有拓扑邻接、拓扑关联、拓扑包含等几种。 拓扑数据结构中关键就是对这些拓扑要素间的拓扑关系进行表示，几何数据的表示可参照矢量数据的简单数据。 虽然，目前GIS中基本拓扑关系的表示方法不尽相同，但是只要能完整表达出拓扑要素间的基本拓扑关系就可以。

 

目前，人们对拓扑关系的表达进行了大量研究，提出了更复杂的关联和邻接关系，但各种GIS软件对矢量空间数据拓扑关系的表达还没有超过使用上述所列的各种关系。

实际上，许多GIS系统在处理使用上述表格的方式有所不同，对于上述出现变长记录的表格（如结点关联的弧段），有的系统使用指针方法，有的则直接存储变长记录(如ArcGIS)。

拓扑数据结构的构建实际上大大增加了数据编辑的难度和复杂性。 以至于它成了一个引起广泛争议的问题。

显然，拓扑关系的存在为数据错误的查找和空间分析提供了必要的前提，但并不是所有的GIS应用、都必须具备这种预先存储的、耗费大量精力才能创建的数据结构。

许多GIS软件只使用其中几种最基本的拓扑关系，就能满足大多数的空间分析需要，但更复杂的空间分析，也许需要更多的拓扑关系。 一般地，建立的拓扑关系越多，数据编辑的维护难度就越大、越复杂， 但进行处理比较复杂的空间分析时就越方便，空间分析花费的时间就越少。 因此，究竟是否应预先存储拓扑关系、存储哪些拓扑关系就成为当前争论的焦点。